优化算法之最小二乘法

2024/04/07

原链接：【PyTorch深度学习】Lesson 5.深度学习的机器学习基础_哔哩哔哩_bilibili

在PyTorch中，最核心的基础数学工具就是梯度计算工具，也就是PyTorch的AutoGrad（自动微分）模块。对于任何一个通用的深度学习框架，都会提供许多自动优化的算法和现成的loss function，PyTorch也不例外。AutoGrad模块，就是PyTorch提供的最核心的数学工具模块，我们可以利用其编写一系列的最优化方法，当然，要使用好微分工具，就首先需要了解广泛应用于机器学习建模的优化思想。所谓优化思想，指的是利用数学工具求解复杂问题的基本思想，同时也是近现代机器学习算法在实际建模过程中经常使用基础理论在实际建模过程中，我们往往会先给出待解决问题的数值评估指标，并在此基础之上构建方程、采用数学工具、不断优化评估指标结果，以期达到可以达到的最优结果。

希望在二维空间中找到一条直线，来拟合这两个点，也就是所谓的构建一个线性回归模型，我们可以设置线性回归方程如下：

$y=ax+b\\\\$

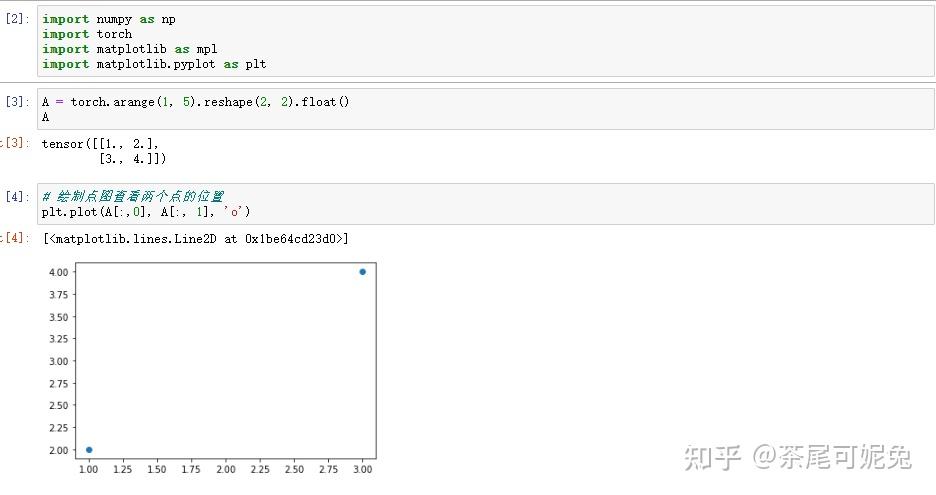
上述问题除了可以使用矩阵方法求解以外，还可以将其转化为最优化问题，然后通过求解最优化问题的方法对其进行求解。总的来说，最优化问题的转化分为两步，其一是确定优化数值指标，其二则是确定优化目标函数。在大多数问题中，这二者是相辅相成的，确定了优化的数值指标，也就确定了优化的目标函数。如果我们希望通过一条直线拟合二维平面空间上分布的点，最核心的目标，毫无疑问，就是希望方程的预测值和真实值相差较小。假设真实的y值用y表示，预测值用?表示，带入a、b参数，则有数值表示如下：

当然，此处我们只带入了（1， 2）和（3， 4）两个点来计算SSE，也就是带入了两条数据来训练y=ax + b这个模型。至此，我们已经将原问题转化为了一个最优化问题，接下来我们的问题就是，当a、b取何值时，SSE取值最小？值得注意的是，SSE方程就是我们优化的目标方程（求最小值），因此上述方程也被称为目标函数，同时，SSE代表着真实值和预测值之间的差值（误差平方和），因此也被称为损失函数（预测值距真实值的损失）.

换而言之，就是当SSE取值最小时，a、b的取值，就是最终线性回归方程的系数取值。
值得注意的是，目标函数和损失函数并不完全等价，但大多数目标函数都由损失函数构成。

在机器学习领域，大多数优化问题都是围绕目标函数（或者损失函数）进行求解。在上述问题中，我们需要围绕SSE求最小值。SSE是一个关于a和b的二元函数，要求其最小值，需要借助数学工具，也就是所谓的最优化方法。选择优化方法并执行相应计算，可以说是整个建模过程中最核心也是相对较难的部分，很多时候这个过程会直接决定模型的性能。

图形展示目标函数

函数的凹凸性

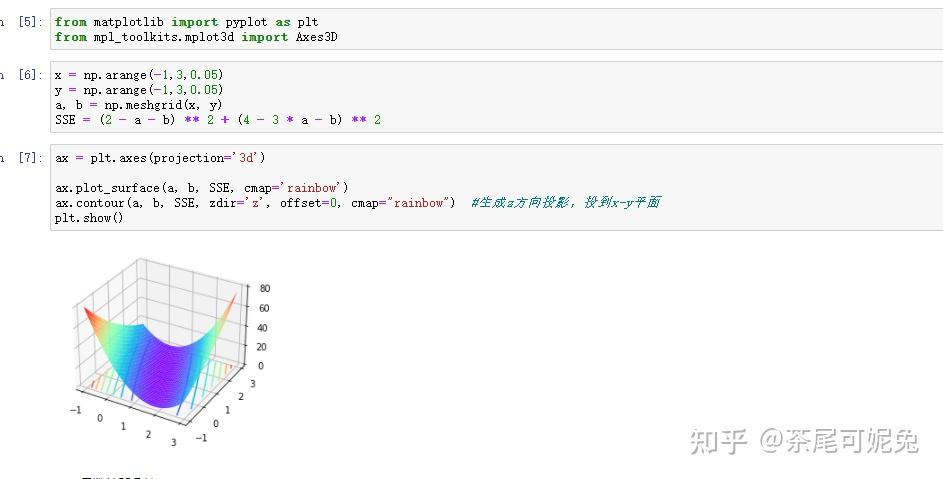
对于一个凸函数来说，全域最小值明显存在，基于凸函数的数学定义，我们可以进一步给出求解上述SSE凸函数最小值的一般方法，也就是著名的最小二乘法

凸函数的最小值

SSE最小值

利用偏导等于0得出的方程组求解线性回归方程参数，就是最小二乘法求解过程。此处我们求得a=1，b=1时，SSE(a,b)取得最小值，也就是（1，1）是目标函数的最小值点。

根据上文内容，机器学习的建模思路可以将其总结如下：

如本节中，我们试图利用一条直线（y=ax+b）去拟合二维平面空间中的点，这里我们所使用的这条直线，就是我们提出的基本模型。而在深度学习中，还将看到更为强大、同时也更加通用的神经网络模型。不同的模型能够适用不同的场景，在提出模型时，我们往往会预设一些影响模型结构或者实际判别性能的参数，如简单线性回归中的a和b；

接下来，围绕建模的目标，需要合理设置损失函数，并在此基础之上设置目标函数，当然，在很多情况下，这二者是相同的。例如，在上述简单线性回归中，我们的建模目标就是希望y=ax+b这条直线能够尽可能的拟合(1,2)、(3,4)这两个点，或者说尽可能“穿过”这两个点，因此我们设置了SSE作为损失函数，也就是预测值和真实值的差值平方和。当然，在计算过程中不难发现，SSE是一个包含了a和b这两个变量的方程，因此SSE本身也是一个函数（a和b的二元函数），并且在线性回归中，SSE既是损失函数（用于衡量真实值和预测值差值的函数），同时也是我们的目标函数（接下来需要优化、或者说要求最小值的函数）。这里尤其需要注意的是，损失函数不是模型，而是模型参数所组成的一个函数。

目标函数既承载了我们优化的目标（让预测值和真实值尽可能接近），同时也是包含了模型参数的函数，因此完成建模需要确定参数、优化结果需要预测值尽可能接近真实值这两方面需求就统一到了求解目标函数最小值的过程中了，也就是说，当我们围绕目标函数求解最小值时，也就完成了模型参数的求解。当然，这个过程本质上就是一个数学的最优化过程，求解目标函数最小值本质上也就是一个最优化问题，而要解决这个问题，我们就需要灵活适用一些最优化方法。当然，在具体的最优化方法的选择上，函数本身的性质是重要影响因素，也就是说，不同类型、不同性质的函数会影响优化方法的选择。在简单线性回归中，由于目标函数是凸函数，根据凸函数性质，判断偏导函数取值为0的点就是最小值点，进而完成a、b的计算（也就是最小二乘法），其实就是通过函数本身的性质进行最优化方法的选取。

利用优化方法求解目标函数，其实是机器学习建模过程中最为核心的环节，因此有必要将围绕上述简单线性回归问题，进一步讨论最小二乘法背后的数学逻辑和优化思想，同时简单探讨数据的矩阵表示方法和基本矩阵运算。虽然最小二乘法并不是主流的深度学习损失函数的优化算法，但从最小二乘法入手了解优化算法背后的数学逻辑，却是非常有必要，同时，线性方程也是构建神经网络模型的基础，因此有必要深入探讨线性模型建模细节以及最基本的优化算法：最小二乘法。

从更加严格的数学角度出发，最小二乘法有两种表示形式，分别是代数法表示和矩阵表示。我们先看最小二乘法的代数表示方法。

首先，假设多元线性方程有如下形式

$f(x)=w_1x_1+w_2x_2+...+w_dx_d+b\\\\$

令 $w=(w_1,w_2,...w_d)，x=(x_1,x_2,...x_d)$ ，则上式可写为

$f(x)=w^Tx+b\\\\$

在机器学习领域，我们将线性回归自变量系数命名为w，其实是weight的简写，意为自变量的权重。

多元线性回归的最小二乘法的代数法表示较为复杂，此处先考虑简单线性回归的最小二乘法表示形式。在简单线性回归中，w只包含一个分量，x也只包含一个分量，我们令此时的就是对应的自变量的取值，此时求解过程如下

优化目标可写为

$SSE=\\sum^m_{i=1}(f(x_i)-y_i)^2=E_(w,b)\\\\$

通过偏导为0求得最终结果的最小二乘法求解过程为：

$\\begin{align}\\frac{\\partial{SSE_(w,b)}}{\\partial{(w)}}&=2(w\\sum^m_{i=1}x^2_i - \\sum^m_{i=1}(y_i-b)x_i)=0 \\end{align}\\\\$

$\\begin{align}\\frac{\\partial{SSE_(w,b)}}{\\partial{(b)}}&=2(mb - \\sum^m_{i=1}(y_i-wx_i))=0 \\end{align}\\\\$

进而可得

$w=\\frac{\\sum^m_{i=1}y_i(x_i-\\bar{x}) }{\\sum^m_{i=1}x^2_i-\\frac{1}{m}(\\sum^m_{i=1}x_i)^2 }\\\\$

$b=\\frac{1}{m}\\sum^m_{i=1}(y_i-wx_i)\\\\$

$其中，\\bar x=\\frac{1}{m}\\sum^m_{i=1}x_i，x_i为x的均值，并且(x_i,y_i)代表二维空间中的点。$

对于线性方程组来说，矩阵表示是一种更加简洁的表示方式，并且对于支持数组运算的torch来说，线性方程组的矩阵表示也更贴近代码的实际书写形式。

$1*a + b=2\\\\ 3*a + b=4\\\\$

在转化为矩阵表示的过程中，我们令

$A=\\left[\\begin{array}{cccc}1 &1 \\\\ 3 &1 \\\\ \\end{array}\\right]\\\\$

$B=\\left[\\begin{array}{cccc}2 \\\\ 4 \\\\ \\end{array}\\right]\\\\$

$X^T=\\left[\\begin{array}{cccc}a \\\\ b \\\\ \\end{array}\\right]\\\\$

则原方程组可表示为

$A * X^T=B\\\\$

更为一般的情况下，多元线性回归方程为

$f(x)=w_1x_1+w_2x_2+...+w_dx_d+b\\\\$

令

$w=(w_1,w_2,...,w_d,b)\\\\$

$\\hat x=(x_1,x_2,...,x_d,1)\\\\$

$\\hat w$ ：方程系数所组成的向量，并且我们将自变量系数和截距放到了一个向量中，此处 $\\hat w$ 就相当于前例中的a、b组成的向量(a,b)；

$\\hat x$ ：方程自变量和1共同组成的向量；

因此，方程可表示为

$f(x)=\\hat w * \\hat x^T\\\\$

另外，我们将所有自变量的值放在一个矩阵中，并且和此前A矩阵类似，为了捕捉截距，添加一列全为1的列在矩阵的末尾，设总共有m组取值，则

$X=\\left[\\begin{array}{cccc}x_{11}&x_{12}&... &x_{1d}&1 \\\\ x_{21}&x_{22}&... &x_{2d}&1 \\\\ ... &... &... &... &1 \\\\ x_{m1}&x_{m2}&... &x_{md}&1 \\\\ \\end{array}\\right]\\\\$

对应到前例中的A矩阵，A矩阵就是拥有一个自变量、两个取值的X矩阵。令y为因变量的取值，则有

$y=\\left[\\begin{array}{cccc}y_1 \\\\ y_2 \\\\ . \\\\ . \\\\ . \\\\ y_m \\\\ \\end{array}\\right]\\\\$

此时，SSE可表示为：

$SSE=||y - X\\hat w^T||_2^2=(y - X\\hat w^T)^T(y - X\\hat w^T)=E(\\hat w)\\\\$

根据最小二乘法的求解过程，令 $E(\\hat w)$ 对 $\\hat w$ 求导方程取值为0，有

$\\begin{aligned}\\frac{E(\\hat w)}{\\partial{\\boldsymbol{\\hat w}}}&=\\frac{\\partial{||\\boldsymbol{y}- \\boldsymbol{X\\hat w^T}||_2}^2}{\\partial{\\boldsymbol{\\hat w}}}\\\\ &=\\frac{\\partial(\\boldsymbol{y}- \\boldsymbol{X\\hat w^T})^T(\\boldsymbol{y}- \\boldsymbol{X\\hat w^T})}{\\partial{\\boldsymbol{\\hat w}}}\\\\ \\\\ \\because &\\ (A-B)^T=A^T - B^T并且(AB)^T=B^T*A^T \\\\ \\\\ \ herefore& 上式=\\frac{\\partial(\\boldsymbol{y}^T - \\boldsymbol{\\hat w X^T})(\\boldsymbol{y}- \\boldsymbol{X\\hat w^T})}{\\partial{\\boldsymbol{\\hat w}}}\\\\ &=\\frac{\\partial(\\boldsymbol{y}^T\\boldsymbol{y}- \\boldsymbol{\\hat w X^Ty}-\\boldsymbol{y}^T\\boldsymbol{X \\hat w^T}+\\boldsymbol{\\hat wX^T}\\boldsymbol{X\\hat w^T})}{\\partial{\\boldsymbol{\\hat w}}}\\\\ &=0 - \\boldsymbol{X^Ty}- \\boldsymbol{X^Ty}+ 2\\boldsymbol{X^TX\\hat w ^T}\\\\ &=\\boldsymbol{X^TX\\hat w^T}- \\boldsymbol{X^Ty}=0 \\\\ &值得注意的是，在矩阵求导中，a为常数，有如下规则： \\begin{equation}\\\\\\frac{\\partial{a}}{\\partial{A}}=0, \\ \\ \\ \\frac{\\partial{A^TB^TC}}{\\partial{A}}=B^TC, \\ \\ \\ \\frac{\\partial{C^TBA}}{\\partial{A}}=B^TC, \\ \\ \\ \\frac{\\partial{A^TBA}}{\\partial{A}}=(B+B^T)A \\end{equation}\\end{aligned}$

进一步可得

$X^TX\\hat w^T=X^Ty\\\\$

要使得此式有解，等价于 $X^TX$ （也被称为矩阵的交叉乘积crossprod存在逆矩阵，若存在，则可解出

$\\hat w ^T=(X^TX)^{-1}X^Ty\\\\$

回到最初的例子，不难发现，有如下对应关系：

$X=A=\\left[\\begin{array}{cccc}1 &1 \\\\ 3 &1 \\\\ \\end{array}\\right]\\\\$

$y=B=\\left[\\begin{array}{cccc}2 \\\\ 4 \\\\ \\end{array}\\right]\\\\$

$\\hat w ^T=X^T=\\left[\\begin{array}{cccc}a \\\\ b \\\\ \\end{array}\\right]\\\\$

手动实现代码验证最小二乘法

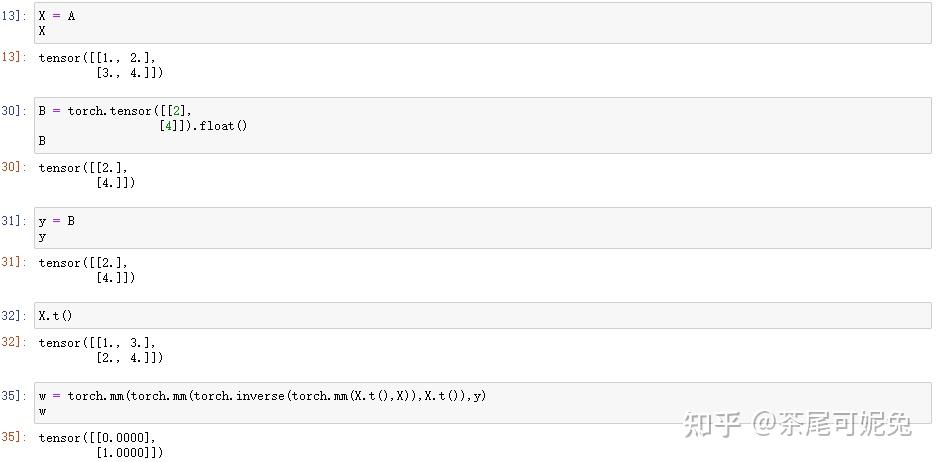
和此前结果保持一致。当然，最小二乘法作为最优化问题的求解方法，我们可以这么理解w最终取值：当w取值为（1，1）时，自变量为w的SSE函数取得全域最小值。

也可以直接调用最小二乘法函数torch.lstsq(B, A)进行求解,对于lstsq函数来说，第一个参数是因变量张量，第二个参数是自变量张量，并且同时返回结果还包括QR矩阵分解的结果.

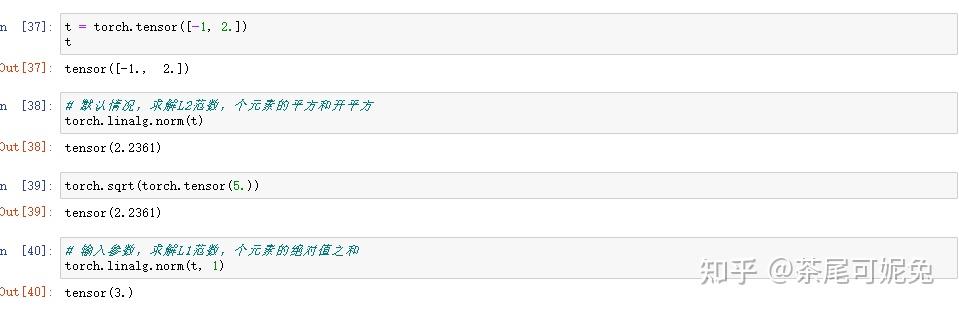
可以反向验证，看下损失函数SSE在a=1，b=1时偏导数是否都为0。此时就需要借助PyTorch中的autograd模块来进行偏导计算。严格意义上来讲，autograd模块是PyTorch中的自动微分模块，我们可以通过autograd模块中的函数进行微分运算，在神经网络模型中，通过自动微分运算求解梯度是模型优化的核心。

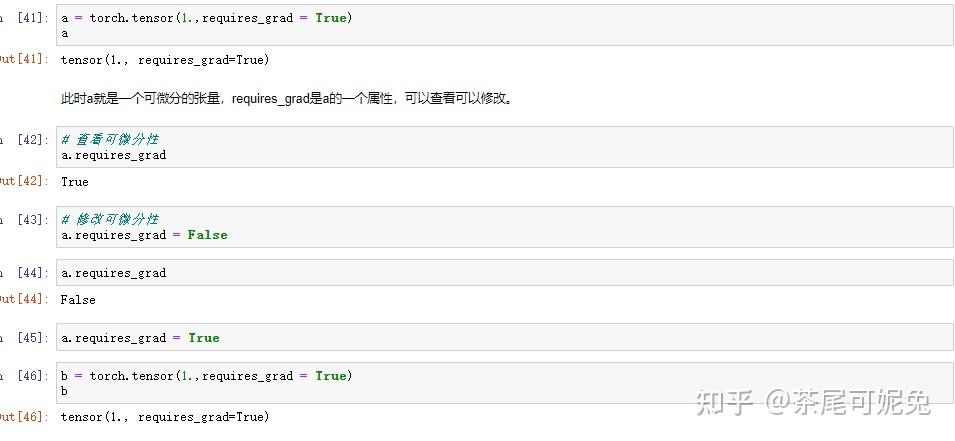
然后创建损失函数

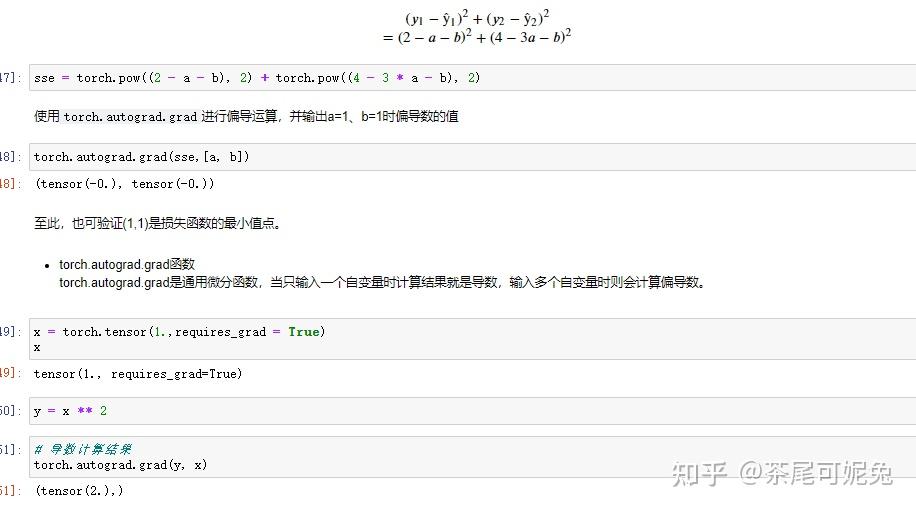
pytorch入坑一 | Tensor及其基本操作 - 知乎 (zhihu.com)

pytorch入门总结指南（1）—import torch as np - 知乎 (zhihu.com)

pytorch入门总结指南（2）—tensor的一些注意事项和autograd+function - 知乎 (zhihu.com)

pytorch入门总结指南（3）—torch的定义nn的几种方式总结 - 知乎 (zhihu.com)

上一篇：持续优化法治化营商环境

下一篇：以营商环境之优助推川渝经济高质量发展

优化算法之最小二乘法

友情链接：